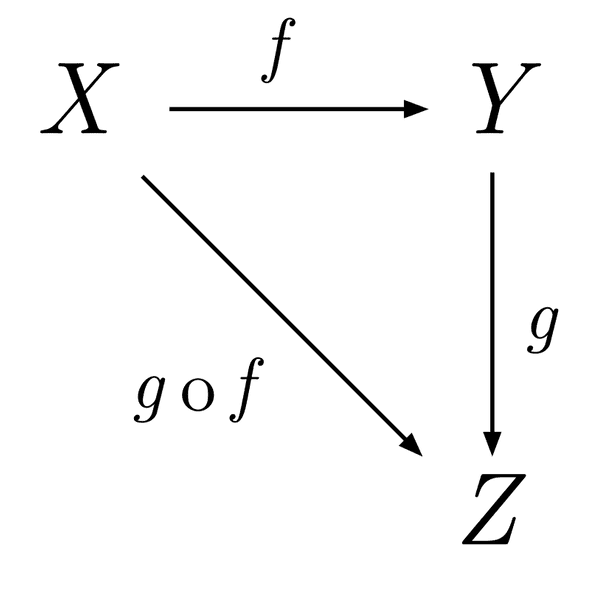Componiendo funciones en JavaScript

Para crear aplicaciones que resuelvan problemas complejos, debemos dividir estos en problemas pequeños que podamos resolver e implementar, luego componemos estas soluciones. Esto es lo que hacemos cada día como programadores y hoy veremos como hacer esto usando funciones en JavaScript.

Nota: Este contenido lo publiqué primero en mi newsletter, la semana después de publicar el newsletter publico en mi blog, si quieres ser el primero en leer suscríbete.

Desde que se inventaron las sub-rutinas o la programación estructural usamos este concepto de crear bloques de código que podamos componer, en programación orientada a objetos todo es componer objetos.

Composición es la esencia de la programación.

En lenguajes funcionales se compone usando funciones, las ideas teorías que sirven como base para esto también las podemos implementar en JavaScript.

Componiendo en JavaScript

Componer funciones se basa en combinar funciones simples para construir funciones más complicadas, para hacer esto el resultado de cada función es pasado como argumento de la siguiente.

“La composición de funciones es el acto de dirigir el resultado de una función, a la entrada de otra, creando una nueva función” Haskell Wiki

JavaScript al implementar funciones de alto orden y closures hace que esto sea bastante sencillo de lograr, podemos escribir esto como:

const compose = (f, g) => (x) => f(g(x));

Con la función anterior podemos componer una función con dos funciones, para hacerlo con más funciones podemos reescribir esta función o usar una librería como Ramda, que tienen un método compose, este nos permite componer una función con X cantidad de funciones.

En matemáticas, la composición de una función es definida como: (f ◦ g)(x) = f (g(x)).

Debemos tener claro:

• Las funciones se ejecutan de derecha a izquierda según se pasen a la función compone.
• El tipo de dato que resulta de una función, debe ser el mismo que acepta como entrada la siguiente función.

La idea principal es que cada función resuelva un pequeño problema y luego componemos una función que resuelva lo que deseamos hacer.

Veamos como funciona con código.

Para las siguientes funciones vamos a usar una lista de datos que puedes ver en este link.

Caso 1

// Calcular el promedio de ingresos de todos los usuarios.
import { prop, map, reduce, add, compose } from 'ramda';
const average = (xs) => reduce(add, 0, xs) / xs.length;
const incomesAverage = compose(average, map(prop('incomes')));
incomesAverage(USERS) // 8333.333

• Las funciones que reciben más de un argumento deben estar currificadas.
• Es una buena idea separar las funciones puras de las que tienen efectos secundarios.

Caso 2

// Retornar el nombre del usuario con mejores ingresos 
import { compose, sortBy, prop, last } from 'ramda';
const bestIncomes = compose(prop('name'), last, sortBy(prop('incomes')));
bestIncomes(USERS); // Laura Mantilla

• Los datos fluyen de derecha a izquierda en las funciones, cada función procesan los datos que recibe.

Caso 3

/*
 * Retornar los nombre en minúscula y
 * reemplazando espacios por underscores(_)
 */
import { compose, replace, toLower, prop, map } from 'ramda';
const underscore = replace(/\s/g, '_')
const nameToLower = compose(toLower, prop('name'))
const toCamelCase = map(compose(underscore,namesToLower))

toCamelCase(USERS) 
// ['yeison_daza', 'camilo_suarez', 'laura_mantilla']

• Una clave de la composición es que podemos agrupar las funciones como deseemos y ir componiendo funciones cada vez más complejas.

Caso 4

/*
 * Comprobar si alguien es un usuario
 */
import { contains, map, prop, compose } from 'ramda';
const toUsers = map(prop('nick'));
const isUser = function(user, data) { 
    return compose(contains(user), toUsers)(data);
}
isUser('yeion7', USERS); // true
isUser('nata1', USERS); // false

• Cada función debe esperar solo un argumento y operar sobre el, por esto es importante trabajar con funciones currificadas.

Funciones genéricas

Para componer funciones es importante pensar en procesar datos abstractos, es decir una función va a procesar un tipo de dato, pero no sabemos que dato sera. A este estilo se llama point free, veamos este ejemplo tomado de mostly adequate guide.

// No es point free porque esta especificando que es una palabra lo que espera
var snakeCase = function(word) {
  return word.toLowerCase().replace(/\s+/ig, '_');
};
// Si es pointfree
var snakeCase = compose(replace(/\s+/ig, '_'), toLowerCase);

De esta manera tenemos funciones genéricas.

Lo que buscamos con esto es crear piezas de código que al implementarlas no pensamos en detalles de su funcionamiento, solo nos enfoquemos en que tipos acepta y retorna.

No con todas las funciones podemos hacer esto, pero es importante buscar crear funciones de este estilo.

La próxima semana hablare sobre como documentar estas funciones.

Teoría de categorías

La composición de funciones esta fundamentada en la teoría de categorías, las ideas de estas han sido utilizadas por la comunidad de programación funcional durante mucho tiempo.

Una categoría se puede representar como:

Esta categoría esta compuesta por:

• Objetos, son datos de cualquier tipo (String, Boolean, Number, etc), en este caso X, Y, Z
• Morfismos, son funciones puras, en este caso f, g
• Composición de los morfismos, en este caso una función compuesta por f y g
• Morfismo llamado identidad, cada objeto tiene una función que retorna su mismo valor.

Propiedades

• La composición es asociativa: Si tienes tres funciones o más, se pueden agrupar de cualquier manera.

h∘(g∘f) = (h∘g)∘f = h∘g∘f

No importa como agrupemos los elementos el resultado siempre va a ser el mismo

• Cada objeto tiene una función identidad: La identidad es una función que retorna el mismo valor que recibe.

const identity = (x) => x;

En teoría de categorías no es importante ver como funciona cada objeto por dentro, todo lo que nos interesa saber es como se relacionan con otros.

No todos los objetos pueden ser compuestos, el tipo que produce el morfismo debe ser el mismo que recibe el siguiente morfismo.

Conclusiones

El saber descomponer un problema en pequeños problemas que podamos resolver es fundamental.

Creo que la composición es una excelente manera de escribir código elegante y mantenible, creando piezas de código que son del tamaño adecuado con las cuales creamos procesos que podemos entender.

También nos ayuda a manejar los efectos secundarios, los cuales podemos separar y saber en donde se ejecutan estos.